Angle trisection

Angle trisection is a classic problem of compass and straightedge constructions of ancient Greek mathematics. It concerns construction of an angle equal to one-third of a given arbitrary angle, using only two tools: an un-marked straightedge, and a compass.

With such tools, the task of angle trisection is generally impossible, as shown by Pierre Wantzel (1837). Wantzel's proof relies on ideas from the field of Galois theory—in particular, trisection of an angle corresponds to the solution of a certain cubic equation, which is not possible using the given tools. Note that the fact that there is no way to trisect an angle in general with just a compass and a straightedge does not mean that it is impossible to trisect all angles: for example, it is relatively straightforward to trisect a right angle (that is, to construct an angle of measure 30 degrees).

It is, however, possible to trisect an arbitrary angle, but using tools other than straightedge and compass. For example, neusis construction, also known to ancient Greeks, involves simultaneous sliding and rotation of a marked straightedge, which can not be achieved with the original tools. Other techniques were developed by mathematicians over centuries.

Because it is defined in simple terms, but complex to prove unsolvable, the problem of angle trisection is a frequent subject of pseudomathematical attempts at solution by naive enthusiasts. The "solutions" often involve finding loopholes in the rules, or are simply incorrect.[1]

Contents

Background and problem statement

Using only an unmarked straightedge and a compass, Greek mathematicians found means to divide a line into an arbitrary set of equal segments, to draw parallel lines, to bisect angles, to construct many polygons, and to construct squares of equal or twice the area of a given polygon.

Three problems proved elusive, specifically, trisecting the angle, doubling the cube, and squaring the circle. The problem of angle trisection reads:

Construct an angle equal to one-third of a given arbitrary angle, using only two tools:

  1. An un-marked straightedge, and
  2. a compass.

Proof of impossibility

The geometric problem of angle trisection can be related to algebra—specifically, to the problem of finding the roots of a cubic polynomial—since by the triple-angle formula, 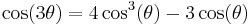\cos(3\theta)=4\cos^3(\theta)-3\cos(\theta).

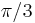One can show that any number constructible in one step from a field K is a solution of a second-order polynomial. Note also that \pi/3 radians (60 degrees, written 60°) is constructible. We now show that it is impossible to construct a 20° angle; this implies that a 60° angle cannot be trisected, and thus that an arbitrary angle cannot be trisected.

Denote the set of rational numbers by Q. If 60° could be trisected, the minimal polynomial of cos(20°) over by Q would be of second order. Now let y = cos(20°).

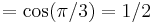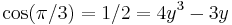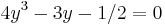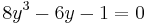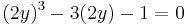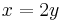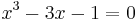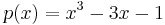Note that cos(60°)= \cos(\pi/3) = 1/2. Then by the triple-angle formula, \cos(\pi/3)= 1/2 = 4y^{3} - 3y and so 4y^{3} - 3y - 1/2 = 0. Thus 8y^{3} - 6y - 1 = 0, or equivalently (2y)^{3} - 3(2y) - 1 = 0. Now substitute x = 2y, so that x^{3} - 3x - 1 = 0 . Let p(x) = x^{3} - 3x - 1.

The minimal polynomial for x (hence cos(20°)) is a factor of 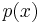p(x). Because 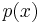p(x) is degree 3, if it is reducible over by Q then it has a rational root. By the rational root theorem, this root must be 1 or −1, but both are clearly not roots. Therefore 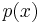p(x) is irreducible over by Q, and the minimal polynomial for cos(20°) is of degree 3.

So an angle of 60° = (1/3)π radians cannot be trisected.

Many people (who presumably are unaware of the above result, misunderstand it, or incorrectly reject it) have proposed methods of trisecting the general angle. Some of these methods provide reasonable approximations; others (some of which are mentioned below) involve tools not permitted in the classical problem. The mathematician Underwood Dudley has detailed some of these failed attempts in his book The Trisectors.[2]

Angles which can be trisected

However, some angles can be trisected. For example, for any constructible angle \theta, the angle 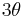3\theta can be trivially trisected by ignoring the given angle and directly constructing an angle of measure \theta. There are also angles which, while non-constructible, are trisectible when given. For example, 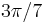3\pi/7 is such an angle: five copies of 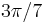3\pi/7 combine to make an angle of measure 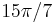15\pi/7, which is a full circle plus the necessary 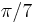\pi/7. 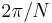More generally, for a positive integer N, an angle of measure 2\pi/N is trisectible if and only if 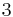3 does not divide N.[3]

One general theorem

Again, denote the rational numbers Q:

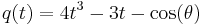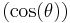Theorem: The angle \theta may be trisected if and only if q(t) = 4t^{3}-3t-\cos(\theta) is reducible over the field extension Q(\cos(\theta)).

The proof is a relatively straightforward generalization of the proof given above that a 60-degree angle is not trisectible.[4]

Trisection using other methods

The general problem of angle trisection is solvable, but using additional tools, and thus going outside of the original Greek framework of compass and straightedge.

By infinite repetition of bisection

Trisection can be achieved by infinite repetition of the compass and straightedge method and based on the binary representation of one-third (.010101...). The angle is bisected, then based on the binary fraction, a choice is made of what angle to bisect next. This algorithm is very similar to computer science's binary search and works for any fraction, even irrational ones.

Using origami

Main article: Mathematics of origami#Trisecting an angle

Trisection, like many constructions impossible by ruler and compass, can easily be accomplished by the more powerful (but physically easy) operations of paper folding, or origami. Huzita's axioms (types of folding operations) can construct cubic extensions (cube roots) of given lengths, whereas ruler-and-compass can construct only quadratic extensions (square roots).

With an auxiliary curve

There are certain curves called trisectrices which, if drawn on the plane using other methods, can be used to trisect arbitrary angles.[5]

With a marked ruler

Another means to trisect an arbitrary angle by a "small" step outside the Greek framework is via a ruler with two marks a set distance apart. The next construction is originally due to Archimedes, called a Neusis construction, i.e., that uses tools other than an un-marked straightedge.

This requires three facts from geometry (at right):

  1. Any full set of angles on a straight line add to 180°,
  2. The sum of angles of any triangle is 180°, and,
  3. Any two equal sides of an isosceles triangle will meet the third in the same angle.

At the diagram at right, angle a (left of point B) is the subject of trisection. First, a point A is drawn at an angle's ray, one unit apart from B. A circle of radius AB is drawn.

Then, the markedness of the ruler comes into play: it is "anchored" at point A, and slided and rotated until one mark is at point C, and one at point D, i.e., CD = AB. A radius BC is drawn as obvious. That is to say, line segments AB, BC, and CD all have equal length. (Segment AC is irrelevant.) Now, Triangles ABC and BCD are isosceles, thus (by Fact 3 above) each has two equal angles.

Hypothesis: Given AD is a straight line, and AB, BC, and CD are all equal length,

Conclusion: angle 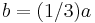b = (1/3) a .

Proof:

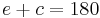  1. From Fact 1) above, e %2B c = 180°.
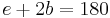  2. Looking at triangle BCD, from Fact 2) e %2B 2b = 180°.
  3. From the last two equations, c = 2b.
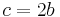  4. From Fact 2), 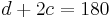d %2B 2c = 180°, thus 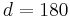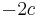d = 180° - 2c , so from last, d = 180° - 4b.
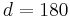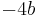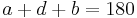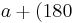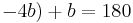  5. From Fact 1) above, a %2B d %2B b = 180°, thus a %2B (180° - 4b) %2B b = 180°.

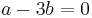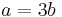Clearing, a - 3b = 0 , or a = 3b , and the theorem is proved.

Again, this construction stepped outside the framework of allowed constructions by using a marked straightedge. There is an unavoidable element of inaccuracy in placing the straightedge.

With a string

Thomas Hutcheson published an article in the Mathematics Teacher[6] that used a string instead of a compass and straight edge. A string can be used as either a straight edge (by stretching it) or a compass (by fixing one point and identifying another), but can also wrap around a cylinder, the key to Hutcheson's solution.

Hutcheson constructed a cylinder from the angle to be trisected by drawing an arc across the angle, completing it as a circle, and constructing from that circle a cylinder on which a, say, equilateral triangle was inscribed (a 360-degree angle divided in three). This was then "mapped" onto the angle to be trisected, with a simple proof of similar triangles.

With a "tomahawk"

A "tomahawk" is a geometric shape consisting of a semicircle and two orthogonal line segments, such that the length of the shorter segment is equal to the circle radius. Trisection is executed by leaning the end of the tomahawk's shorter segment on one ray, the circle's edge on the other, so that the "handle" (longer segment) crosses the angle's vertex; the trisection line runs between the vertex and the center of the semicircle.

Note that while a tomahawk is constructible with compass and straightedge, it is not generally possible to construct a tomahawk in any desired position. Thus, the above construction does not contradict the nontrisectibility of angles with ruler and compass alone.

See also

References

  1. ^ Steven Dutch. "Why Trisecting the Angle is Impossible". University of Wisconsin - Green Bay. http://www.uwgb.edu/dutchs/pseudosc/trisect.htm. 
  2. ^ Dudley, Underwood, The Trisectors, Mathematical Association of America, 1994.
  3. ^ McLean, K. Robin, "Trisecting angles with ruler and compasses", Mathematical Gazette 92, July 2008, 320–323. See also Feedback on this article in vol. 93, March 2009, p. 156.
  4. ^ Stewart, Ian (1989). Galois Theory. Chapman and Hall Mathematics. pp. g. 58. ISBN 0412345501. 
  5. ^ Trisection of an Angle
  6. ^ Hutcheson, Thomas W. (May 2001). "Dividing Any Angle into Any Number of Equal Parts". Mathematics Teacher 94 (5): 400–405. 

Additional references

External links

Other means of trisection

Mathematicians
Anaxagoras · Anthemius · Archytas · Aristaeus the Elder · Aristarchus · Apollonius · Archimedes · Autolycus · Bion · Boethius · Bryson · Callippus · Carpus · Chrysippus · Cleomedes · Conon · Ctesibius · Democritus · Dicaearchus · Diocles · Diophantus · Dinostratus · Dionysodorus · Domninus · Eratosthenes · Eudemus · Euclid · Eudoxus · Eutocius · Geminus · Heron · Hipparchus · Hippasus · Hippias · Hippocrates · Hypatia · Hypsicles · Isidore of Miletus · Leo the Mathematician · Marinus · Melissa · Menaechmus · Menelaus · Metrodorus · Nicomachus · Nicomedes · Nicoteles · Oenopides · Pappus · Perseus · Philolaus · Philon · Porphyry · Posidonius · Proclus · Ptolemy · Pythagoras · Serenus  · Simplicius · Sosigenes · Sporus · Thales · Theaetetus · Theano · Themistoclea · Theodorus · Theodosius · Theon of Alexandria · Theon of Smyrna · Thymaridas · Xenocrates · Zeno of Elea · Zeno of Sidon · Zenodorus
Treatises
Centers
Influences
Influenced
Tables
Problems